【1】はじめに

筆者の勤務する東京都立町田高等学校（以下「本校」という）では現在、情報Aを1学年で2単位実施している。新カリキュラムにおいては、問題解決学習をより重視した情報の科学を1学年で全員必履修とする予定である。この稿では、新カリキュラムに向けた問題解決の発展学習として行ったモデル化とシミュレーションの概要と生徒の状況について簡単に報告する。

【2】年間計画の中での位置づけ

2.1 配当時間

情報Aとしての位置づけも考慮し、モデル化に2時間、シミュレーションに1時間の計3時間を配当することとした。

2.2 おおまかな内容

授業では、モデルの種類を一通り意識させた後、図的モデルとして状態遷移図とフローモデルを、また数式モデルとシミュレーションとしては、できるだけ身近な数式モデルを選び、実際に数値を入れて動かしてみるような実践を行った。この考え方のバックグラウンドとして、
● 図解の授業を先取りしたい
● 学校生活での「段取り」をもっと意識させたい
● 表計算ソフトウェアの利用を実践的に行いたい
の3点が挙げられる。

【3】授業実践

3.1 1時限目（モデル化の種類と状態遷移図）

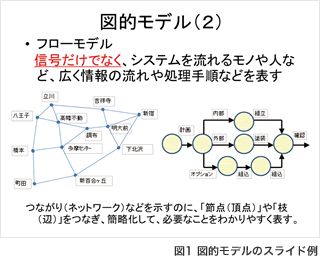
1限目はまず「モデルとは」という形でモデルについての説明をした上で、授業で扱うモデルの分類を確認した。この際、専門教科情報「モデル化とシミュレーション」の教科書にある分類に従い、物理モデル、図的モデル、数式モデルの3種類とした。特に図的モデルでは、ブロック線図、フローモデル、状態遷移図を扱い、状態遷移図、フローモデルについて特にていねいに扱うこととした。一方、動的と静的、連続時間と離散時間、確定的と確率的といった各モデルの分類については、時間の都合上簡単に説明するに留めた。

まずは状態遷移図を扱ったが、これは、例えば温度という入力要素よって冷房、送風、暖房と状態が自動的に切り替わるエアコンなど、身近な生活家電に例えやすく、生徒もイメージしやすいのではないかと考えたからである。実際、温度とエアコンの関係を生徒に答えさせた所、全く問題なく答えることができていた。

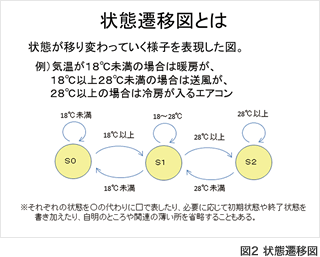この時に注意したことが、記号の利用は状態の名前など最小限にしたことと、いきなり状態遷移図を書くのではなく、まずは必ず状態遷移表を作らせたことである。やはり1学年の段階では、記号が出てきただけで難しさを感じてしまうことが多く、実際、状態の名前をs0、s1などと置いただけで混乱してしまう生徒も若干見られた。また、まずは表に整理させることによって、状態や入力手段の確認ができ、的確な図での表現につながったようにも見られる。

3.2 2時限目（フローモデル）

2時限目は主にフローモデルについて扱った。

無向グラフと有向グラフについての説明後、特に有向グラフについて、川でのバーベキューを例にとって説明をおこなった。これは、遠足でバーベキューをおこなっているため、少しでも身近な材料を提供したいと考えたからである。

有向グラフを扱った理由としては、本校は45分7時間授業のため放課後の時間が短く、生徒は常に時間の効果的・効率的な利用を迫られているからであり、行事への取り組みなども、やるべきことを明確化させ皆で協力して行うことができるような力を身につけさせたかったことによる。

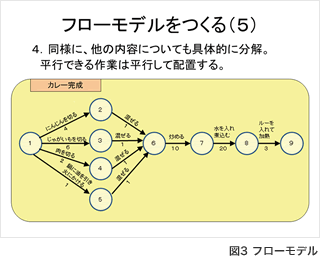
授業では、「かまどを作る」「カレーをつくる」など作業をまずは大まかに分け、それぞれの作業の中でさらに細かく手順を意識し矢印で流れを作っていく方法をとった。最後に練習として「サラダをつくる」フローモデルを書かせたところ、ほぼ全員が完成させることができた。

3.3 3時限目（数式モデルとシミュレーション）

数式モデルでは、グラフの授業で行った散布図と相関関係を利用し、回帰直線を意識させる所を切り口とした。その後、シミュレーションの例として、総務省統計局のWebサイトを利用しての割合による人口増加・減少、預金の複利計算による利息、そして確率的モデルではモンテカルロ法による円周率の計算について扱った。

統計局の人口シミュレーションでは、2000～2001年の人口増加割合に基づく2035年の人口を表計算ソフトを利用して求めさせた。さらに、練習も兼ねて2008～2009年についても同様に計算させ、最後に実際の統計局のWebサイトから統計局の値を確かめさせた。ここでは、数式モデルの立て方によってシミュレーションの結果が変わってくること、そのため、実際のシミュレーションでは、さらに複雑な要因も加味して計算していることに帰着させた。また、預金の複利計算では、複利のしくみを教えるとともに、単利計算と1ヶ月複利の計算を表計算ソフトで行い比較させることによって、表計算ソフトの有用性と消費者教育の双方をねらいとした。

【4】まとめと課題

今回の実践を通して得られた内容と課題として、以下の3点を挙げておく。

【1】手で書くことの重要性

状態遷移図やフローモデルを書かせた時、初めは図解の練習も兼ねてオートシェープを利用させていたが、PCの操作が中心になってしまい内容が定着していない様子が見られた。これは考査の結果からもその傾向がみられている。

【2】表計算ソフトの習熟

シミュレーションを進める上で、表計算ソフトの習熟差による影響が非常に大きい。既に表計算ソフトの利用については学んでいるが、それを別のケースに実践的に応用できる能力をもっともっと身につけさせる必要がある。

【3】数学的な知識の必要性

数式モデルの構築やシミュレーションを進める上で、どうしても数学的内容と切り離せない部分が出てくるが、1学年の段階で得ている知識ではどうしても限界がある。そのため、既得知識の把握や数学科との連携が重要な要素であると考える。

※第4回全国高等学校情報教育研究大会大阪大会要項から転載
（2011年12月掲載）