実践研究「情報科」

「ガチャ」の確率シミュレーション ~情報Ⅰ全体を概観してみて~

武善 紀之教諭
日出学園中学校・高等学校
はじめに
いよいよ新学習指導要領実施の年が迫ってきた。スケジュール通りに進行すれば、来年度には教科書採択、再来年度にはいくつかの現場で情報Ⅰの授業が実際に行われる。プログラミングにデータサイエンスと、盛りだくさんの情報Ⅰについて、扱う内容全体を浅く広く概観できるような実習はないだろうか。
そんな思いのもと、学校再開後、情報Ⅰ「(3)コンピュータとプログラミング」に内包される「シミュレーション」を中心に、「当たり1%のガチャ、100回引くと1回は当たる?」という題材に取り組んでみた。突然の休校に、普段より多くソーシャルゲームのガチャを引いていた生徒もいたことだろう。何気なく引いてしまうガチャだが、実際はどれくらい当たるものなのだろうか?
実習を紹介後、結びでは新学習指導要領のポイントについても迫ってみたい。本実習は、大きく2段階で構成されている。
- シミュレータに向かってクラスみんなでマウスを連打し、
「当たり1%のガチャを100回引く」試行を集めて、分析する。 - Excelに数式を入力して、理論値を調べる。
片方だけでも実習は成立する。しかし、切り口を変えて題材を2度見つめることは、生徒達の理解を促すことに極めて有効だ。
なお、本実習は情報Ⅰ全体を浅く広く概観するという観点から、Step1、Step2で1時間、Step3以降で1時間の計2時間で実施した。生徒によるシミュレータの作成を省略するなどにより、実習時間の短縮も可能である。
Step1.予測する
シミュレーションを実行する前に、生徒達には次のような問いの予想を立てさせよう。
- 当たり1%のガチャを100回引くとき、自分は何回目くらいで最初に当たるか?
- 当たり1%のガチャを、100人がそれぞれ100回ずつ引く。
1回も当たりが出ない人は何人いるだろう?
GoogleフォームやSKYMENUのアンケート機能を活用して、0~100の数値で回答させると、集計作業が楽になる。例えば⑵について、本校では0~10人程度と見積もる生徒が最も多かった。
Step2.シミュレータを作ろう【プログラミングの入り口】
本校の生徒達にとって、テキストコーディングは初めての経験であった。
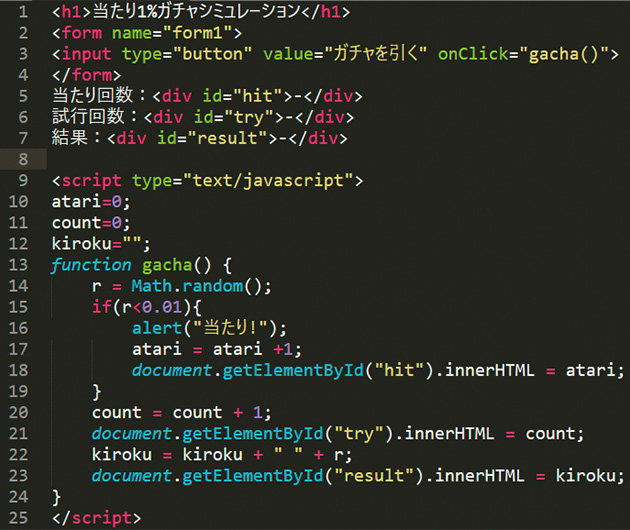
(Sublime Text上で撮影したスクリーンショット)
プログラミング指導の際は、エディタ選びが重要になる。本校ではエディタに、シェアウェアのSublime Textを活用している。このエディタには入力途中のタグについて候補を表示してくれたり、閉じタグを自動で入力してくれたりする自動補完機能や、ソースコードを色分け表示する機能が搭載されている。プログラムの全文をに示す。
授業ではプログラムを「HTML」「Formボタン」「アラート表示」「計算結果表示」「当たり判定」「表示更新」の6つに分割し、ステップ・バイ・ステップで指導した。この説明に関するプリントは、筆者Webページにて公開している参考文献。
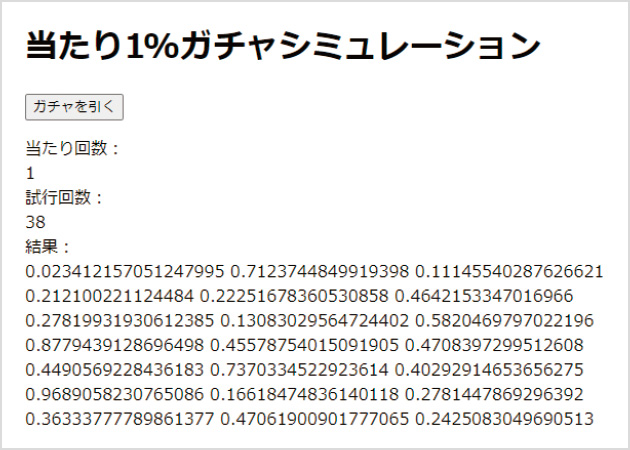
この結果、でき上がるシミュレータがである。「ガチャを引く」ボタンを押すと結果が表示され、1%を引き当てたとき、「当たり!」とアラートが出てくる。短いコードだがif文、変数、乱数、関数といったプログラミングの基本をひととおり体験することができる。

進みの早い生徒には、「課金額」の欄を作成したり、文字色や背景色を変更したりと、自由な改良を行ってもらった。CSSについても踏み込んで扱えば、情報デザインの入り口としても活用できるかもしれない。
Step3.実際にガチャを引いてみよう【データサイエンスの入り口】
いよいよシミュレーションの実行だ。ガチャを100回引き、その際に「当たり」を引いたタイミングと回数について、記録を取る。このとき、集めるデータは100名分程度あると良い。40人クラスであれば、1人に2回(200回)引かせることになる。実際にガチャを引く場面で、クラスは大変盛り上がる。
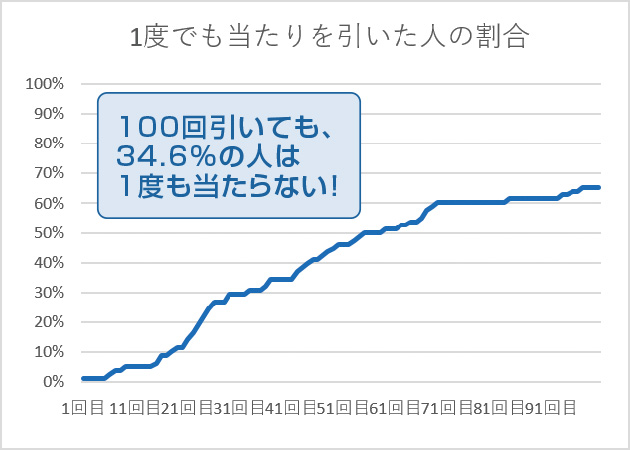
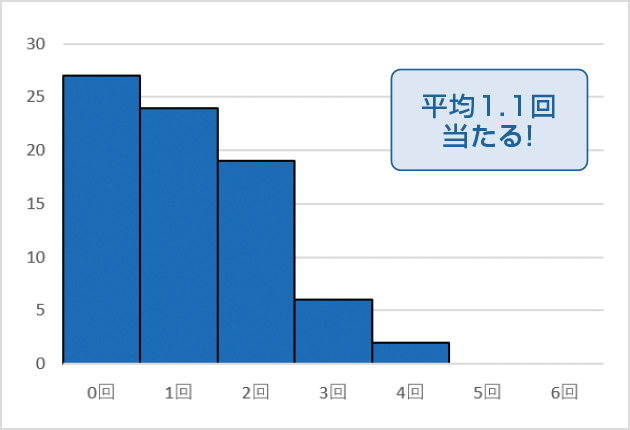
あるクラスで実施した結果を分析したグラフをに示す。この処理は、「折れ線グラフ」や「ヒストグラム」の書き方を学ぶ機会としても利用できる。
- 100回引いても、当たらない人が34.6%もいたこと。
- 当たった回数の平均を取ると約1.1回であったこと。
もちろん数値は実施の度に異なるが、傾向は変わらないはずだ。この2つの結果を、生徒達は驚きと共に迎える。
Step4.理論確率を調べよう【モデル化とシミュレーションの入り口】
Step2、3のように、乱数で値を推定するシミュレーションの方法をモンテカルロ法という。しかし、今回の事例のように出現確率が明確な事象では、表計算ソフトウェアを使って厳密な理論値をシミュレートすることもできる。

モデルに必要な数式は案外単純である。
にExcelの画面を示す。入力する数式は2つだけで、B4セルに「=($B$2)^A4」、C4セルに「=1-B4」と入力し、あとは試行回数分下までオートフィルすればよい。授業では300試行までを計算して、グラフに起こした。
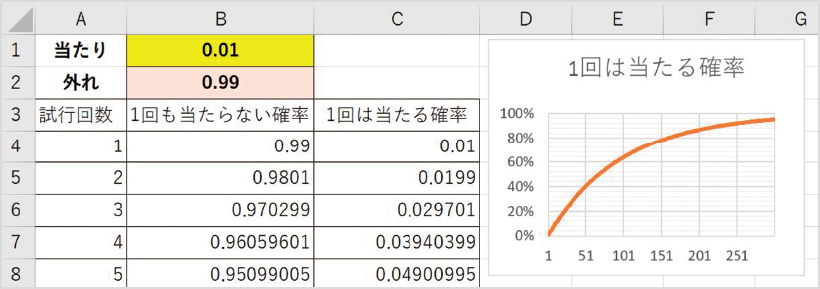
この結果から次のような値が読み取れる。

「当たり1%ガチャなのに、100回引いても36%の人は当たらない」。2度のシミュレーションからこの結論に誤りはなさそうだ。これは私達の直感に反するものだが、を見ると理由がよく分かる。平均的には確かに1.1回当たりが出ている。しかしこれは、みんなが1回当たるということではなく、100回の間には、1回も当たらない人もいれば、3~4回当たる人もいることを意味しているのだ。個人ではなく集団を意識することこそ、高校以降のデータサイエンスの基本となる。
新学習指導要領に向けて
生徒達は実習の最中、常に楽しそうに取り組んでいた。「ガチャ」が生徒達をすでに惹きつけている題材であること、結果が予想に大きく反することなどが理由として挙げられる。しかし、構成にもポイントがある。今回のようにアプローチを2つ用意することで、作業や理解が追いつかない生徒がいても、どちらかの事例が腑に落ちるポイントとして機能するようになる。また、2つのシミュレーションの比較にも発展させられる。本実習を例えば情報Ⅰの最初に行えば、情報Ⅰで扱われる内容について、生徒達は浅く広く概観することができるだろう。
さて、結びとして新学習指導要領に関して私的なポイントを2点挙げてみたい。
まず1点目は、やるべきことが盛りだくさんに詰め込まれているが、各単元間はどれも密接につながっているということである。
本実習に当てはめれば、私達の「本当にそうかな?」を確かめる手段としてプログラミングやシミュレーションがあり(情報Ⅰ(3))、その中で収集したデータを整理、分析していくためにデータサイエンスがある(情報Ⅰ(4))。単元間をどのように結び合わせるかも、1人ひとりの教員の腕の見せ所だ。
2点目は、いわゆる技能だけでなく、従前に比べて大幅に「演算の仕組み」や「値の精度や誤差」といったコンピュータサイエンス的要素が拡充されている点だ。
コンピュータをなぜ問題解決に活用するのか。それはコンピュータと人間が、物事を違うように考えるためだ。今回扱った「1%のガチャは100回引けば1回は当たる」「外れがこれだけ続いたから次は当たりが来る」という思い込みを思い出してほしい。少数試行にこのような思い込みを当てはめてしまうことはギャンブラーの誤謬と呼ばれ、人間はこのような認知バイアスに多く支配されている。しかしこれは、人間が厳密なアルゴリズムで動作するコンピュータに劣っていることを示すわけではない。経験則や先入観で迅速に、直感的に答えを導くヒューリスティックスと呼ばれる思考法で、これは人間の得意技である。
人間とコンピュータそれぞれの特性や長所をよく理解することで、コンピュータ活用の幅は大きく広がっていく。「プログラミング」の必修化に向けてさまざまな研修等が開催されているが、理論について扱われることは案外少ない。再来年度に迫った情報Ⅰの実施に向けて、理論強化と技能習得の両軸で、今後も準備を進めていきたい。
参考文献
- http://high.hinode.ed.jp/share/takeyoshi/n_takeyoshi.html
(2020年12月掲載)
