本時のねらい	曲線を含む形のおよその面積について、既習の公式が活用できる図形にみなして、既習の求積方法で求める考え方について、図や式で説明することができる。（思考・判断・表現）
授業の実際	面積という視点から見れば、日常生活の中には算数で扱うようなシンプルな形は少なく、複雑な形があふれている。このような複雑な形を、およその形にみなして面積を求める学習は、生活と算数が直結していることを感じ取れる、大切な単元である。しかし、およその形のみなし方、計算方法は人それぞれなため、多様に「答え」が存在してしまい、認め合うことに難しさがある。そこで、本学習では「形のみなし方」を認め合う活動を行うことで、どのようにすれば基の図形から離れ過ぎず、計算しやすい形にみなすことができるか考える力を身につけていけるようにする。ここでは、タブレット端末を活用し、友達の「形のみなし方」を一覧で見てどこがよいのか共有したり、計算式から効率性や正確性を判断したりできるようにする。このような学習をとおして、日常生活の中でもいろいろなものを、およその形でみなして思考できる子どもの姿をめざしていく。

単元計画（全3時間）
第1時	複雑な形の面積の求め方（本時）
第2時	いろいろな面積を求めよう
第3時	まとめの練習

本時の展開

学習の流れ	主な学習活動	指導のポイント （タブレット端末活用場面）
導入	1．本時の問題と課題をとらえる。 琵琶湖のおよその面積を求めましょう 今までに習った図形の形ではないね。 およその面積だから、だいたいの形でいいんじゃないかな。 どのように考えれば、簡単に求められるかな	［投影］機能を用いて、教室の前の画面に、何の形なのかをあてるシルエットクイズを投影することで、楽しい雰囲気で学習をスタートさせ、形に注目する学習活動への意欲を高める。
展開1	2．複雑な形の面積の求め方を考える。 長方形とみなして（例：15×55＝825） 直角三角形とみなして（例：55×25÷2＝687） いくつかの四角形に区切って （例：5×15＋10×40＋10×15＝625）	［配付］機能を活用することで、全員が同一の形を基に考えを記入していけるようにする。また、計算式を記入するスペースを意図的に設けておき、効率的に計算できる考え方を促していく。
展開2	3．友達の求め方を見て、良い点を伝え合う。 すごく簡単に計算できる方法だね。 本来の面積にとても近い数値が出せるね。 一番正確な方法はどれなんだろうな。	［みんなの作品］機能を活用して、友達の考えを共有したり、その良さをデジタル付箋で伝え合ったりすることで、多様な「形のみなし方」に気づけるようにする。
終末	4．本時のまとめを行う。 私の方法よりも、友達のほうが、計算がとても簡単な方法になっていたよ。 あまり簡単な形にし過ぎても、本来の面積からの差が大きくなるよね。	［みんなの作品］の［比較表示］機能を活用して、いろいろな「形のみなし方」を比較表示することで、算数として効率的な方法はどれかという視点で、考えを練り上げていけるようにする。

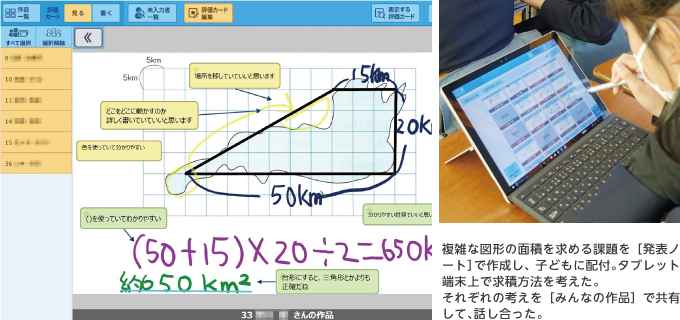
子どもたちは、配付されたシートに思い思いの考えを入力していった。配置した図形は背景化していたため、子どもたちの操作には干渉されないようになっており、直接図形の上に線を引いたりしながら、どんな形とみなすのか、いろいろと試していた。また図形の隣に意図的にスペースを空けていたため、そこに言葉を書き添えて説明したり、計算式を記入したりする子どもの姿が見られた。

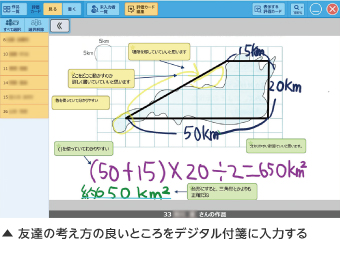
先ほど入力したシートを［みんなの作品］に提出すると、自由に確認しあえるようになる。子どもたちは、多様に広がる友達の考え方を見ながら、「この計算は簡単だね」「細かい形に区切れば正確な数値が出せるね」などと、それぞれの良さを認め合っていた。さらに、デジタル付箋を貼れるため、友達から認められたことが文字として記録に残る。子どもたちがうれしそうに自分のシートに貼られたデジタル付箋を見つめる姿が印象的だった。

多様な考え方を認め合った子どもたちは、計算を簡単にする考え方と、本来の面積から離れないようにする考え方があることに気づいた。そこで、［画面一覧］を用いて、それぞれの計算式を表示しながら、「複雑な形に区切って計算したら、結局形をみなす意味がない」「いくら計算を簡単にしても、本来の面積からかけ離れては意味がない」などと比較検討した。算数ではどちらも大切な視点で、両立できる方法を探すことを学んだ。

（2019年7月掲載）