本時のねらい	本時は、ドット（●）の数の求め方をまとめるなどして工夫して考え、1つの式に表すことをねらいとしている。また、式の意味について考える活動を通して、それぞれの式に共通していることを発見することで、「●の数が増えてもできるよ」や「もし四角だったら」などの発言を引き出し、関数的な見方に触れることもねらいとした。
授業の実際	1辺に9個ずつ三角の形（頂点の部分が重なっている）になっているドット図を提示した。ここで、「1つずつ数えなくてもできるよ」という発言を引き出し、「かけ算を使えば1つの式にできるよ」という問いが生まれた。 児童は、配付された［発表ノート］に式と考え方を説明するための図を記入していった。発表する場面では、考えた図からみんなで式を話し合ったり、1つの式からそれに対応する図を完成させたりする活動を行った。 学習の終末では、「この形だったから1つの式にできたのだね」と問いかけると、式について振り返り、その共通点から言葉の式に表すことで、関数的に考えることができた。

単元計画（全7時間）
第1時	（　　）を用いた式
第2・3時	四則混合の式と計算
第4時	1つの式に表す（本時）
第5時	分配法則
第6時	交換法則、結合法則
第7時	乗法の性質

本時の展開

学習の流れ	主な学習活動	指導のポイント （タブレット端末活用場面）
課題をつかむ	1.ドットの数を1つの式で表すという問いをもつ。 2.タブレット端末の操作の仕方について確認する。	電子黒板に［発表ノート］の画面を提示する。
解決する	3.タブレット端末を操作して、式と図を考える。 4.式と図について発表し合い、式と図と言葉を対応させながら理解する。	児童が1人ひとりタブレット端末で操作し、コピーしながら多くの考えをまとめる。
まとめる	5.式を見比べて、どの式も辺の数と1辺のドットの数を使って計算していることを捉える。	児童の画面を電子黒板に提示する。
振り返り、新たな課題をつかむ	6.学習したことを振り返り、形や数が変わってもドットの数を計算で求められるか考える。

ドット図は、一度にすべて見せるのではなく、予め貼り付けておいた青色の図形を動かすことで、少しずつ見せるようにした。これにより、「全部見せて」や「全部見なくても分かるよ」などの児童同士の対話が生まれ、「だって、1辺の数が分かれば…」「1つの式に表せそうだね」という問いを共有することができた。教師から与えられた目標や課題ではなく、自分たちで目標を立てることにつながった。

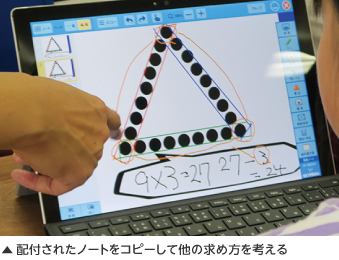
予め作成しておいた［発表ノート］を児童に配付した。このノートは、予めドット図と式を記入する枠を入れてあるものである。プリントで配布して回収したり、自分で手書きしたりする手間が省略でき、「1つの式で表す」という目標に短時間で迫ることができた。また、コピーして使用することで、自分の考えを早くまとめられた児童は、「他の式もできる」と多くの式と図にまとめることができた。

［発表ノート］の［提出］の後、それぞれの考え方について話し合う場面では、1つの考え方を1人の児童に発表させるのではなく、式のみ発表させた。学級全体で式の意味を図に記入しながら1つずつ理解していった。また、図だけ見せて、そこから考えられる式を発表し合う活動も行った。最後に、提出された［発表ノート］を一覧で表示し、それぞれの考え方を確認した。この活動により、式をより正確に理解でき、学習の終末に「形が変わってもできる」という新たな問いを生み出すことにつながった。

（2019年2月掲載）