本時のねらい	本時で取り上げる立体は、一見「底面積×高さ」が使えないように見える。だが、底面をL字の部分として見れば、角柱として見ることができる。そこで、ねらいを「底面が複雑な図形の体積も角柱とみて、底面積×高さの式で求められることを理解する」と設定した。
授業の実際	児童に立体の模型を提示し、どのような方法で体積を求めるかについての見通しを持たせた。ここでは、5年時における「分解、合成」の考え方が出ていた。前時までの既習内容である「底面積×高さ」は使えないかということを問うたところ、立て方を変えれば求められるという反応が返ってきた。そこで、複雑な立体でも「底面積×高さ」は使えるのかを検証していくこととした。 まずは、4人のグループで役割を決め、どの考え方で解くかを決めさせた。その後、発表ノートに個人の考えを記述させ、［画面合体］機能で4人の考えの合体を行った。合体後、すぐに解除することによって、自身の手元に4人の考えが集約されたスライドが戻ってくる。児童らは、このスライドをもとに、複数の考えを比較するなかで、複雑な立体でも「底面積×高さ」は使えるということに気が付いていた。

単元計画（全5時間）
第1次	・ 四角柱の体積の求め方とは
	・ 三角柱の体積の求め方とは
	・ 円柱の体積の求め方とは
	・ 底面が複雑な立体の体積の求め方とは（本時）
第2次	・ 確認問題を解く

本時の展開

学習の流れ	主な学習活動	指導のポイント （タブレット端末活用場面）
課題をつかむ	課題 複雑な立体の体積を求めるには！？ ～ 底面積×高さは使えるのか ～	見通しをもつことができるように平面図だけではなく、立体模型も提示する。
見通しをもつ	見通しをもとに個人で考えを持つ。各班4人で相談し、解き方の役割分担を行う。	5年時の既習内容を活用する考え方と、本単元で学習した考えの2つの考え方をおさえる。
個人で考える	自身が担当する考え方を自身の発表ノートに記述する。	立体図を配付し、個人の考えを書く。
グループで共有する	考えを伝え合い、学習課題について話し合う。	［画面合体］機能を活用し、4人の考えを集約する。
学習をまとめる	学習課題にたちかえり、まとめる。	学習をまとめるために、1つのグループのスライドを電子黒板に投影する。

見通しを持つ段階では、5年時の既習内容である「分解、合成」の考え方と前時までの既習を活かした「底面積×高さ」の考え方の2種類が児童から出てきた。そこで、自分がどの考え方で体積を求めるかについて、グループの中で役割を明確にさせ、複数の考え方がうまれるように配慮した。また、ここでは、複雑な立体のL字の部分を底面として見ることが必要である。そこで、複数の立体図を「発表ノート」に準備しておき、個人で選択させたうえで「発表ノート」に考え方を書かせた。

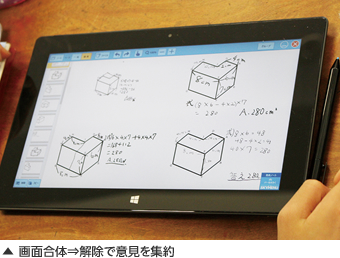［画面合体］機能を活用し、まずは考えが書かれている4人のスライドを合体する。その後、すぐに「画面合体」の解除を行った。このことにより、1枚のスライド上に4人分の考えが集約される。自分の手元にある端末で、全員分の考えを一覧で確認できることから考えの比較が容易となる。一人一人が自身の考えを他者に説明した後に、考えの比較から結果的にどんなことが言えるかを話し合わせた。

学習をまとめる場面では、1つのグループのスライドを電子黒板に投影した。多様な考え方の比較からどんなことが言えたかについての確認を行った。投影したものを、さらに［マーキング］機能で焦点化させることができた。その後、底面が複雑な立体の場合でも、「底面積×高さ」が使えたことを押さえ、多様な考えのなかで、どの考え方が解きやすいかを問うた。児童は、自分の端末を見直し、再度考えを比較していた。

（2016年6月掲載）